International Conference on Field-Programmable Technology - Design Competition

Task

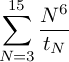Your task for this competition is to develop a general Sudoku solver for an FPGA. The goal of your design is to solve in the shortest possible time a set of general Sudoku puzzles with 3 ≤ N ≤ 15, where N denotes the order of a test puzzle. Your final score will be calculated according to the following formula: $\sum_{N=3}^{15}\frac{N^6}{t_N}\quad\quad \forall t_N \leq 2 \;\text{minute}$ t_N is the average time your solver needs to solve puzzles with order N, correct to the nearest microsecond. Your design will be tested with puzzles with orders in the range of 3 to 15.

Based on this objective function, a design that can solve puzzles with high orders in a short period of time will have a much higher chance of winning than designs that are only able to solve puzzles of small orders. Therefore, you are encouraged to design an FPGA solver that is able to deal with puzzles with as high an order as possible. As a reference, most existing software Sudoku solvers are able to solve puzzles with orders up to N=7 within minutes.

Data Input

The size of the puzzle, N*N, together with the puzzle will be transmitted to your FPGA design through an RS-232 connection using the following format:

0xA5

0x3C

0x5A

0xC3

N*N

d[0,0]

d[0,1]

...

d[N*N, N*N]

checksum

A sequence of four synchronizing bytes will first be transmitted. After that, the number N*N will be transmitted. For example, the number 9 will be transmitted for the standard Sudoku puzzle.

Subsequently, the values of each cell of the puzzle will be transmitted in a row-major fashion, starting from the top-left, going down to bottom-right. A cell value of 0 indicates that a cell is empty. Otherwise, the given value of a cell is transmitted.

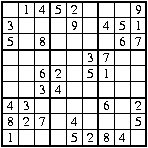
For example, the first puzzle shown in the Background page would be transmitted as:

0xA5

0x3C

0x5A

0xC3

...

checksum

All numerical values are represented as 8-bit unsigned values.

The RS-232 connection should be set to a baud rate of 115200 bps, 8-bit data, no parity bit and 1 stop bit (115200 8N1).

Data Output

Your design should return the solved puzzle to the PC host using the same RS-232 connection and a data format similar to that of the input data, except that all 0's are replaced with the solved value. Also, the checksum byte is transmitted before the solved puzzle. This is to ensure that the time for transmitting the solved puzzle will have minimal effect on the puzzle solving time.

For example, the solution to the puzzle shown above will be transmitted as:

0xA5

0x3C

0x5A

0xC3

checksum

...

Checksum Calculation

The checksum byte for data input and output is calculated against the values of the cells of the transmitted puzzle using the following equation: $\sum_{r=0}^{N^2-1} \sum_{c=0}^{N^2-1} (-1)^{((r + c) \% 2)} d[r,c]$ where d[r,c] denotes the value of a cell at row r and column c, counting from zero.

In other words, the value of the checksum is the sum of the values of all the cells with r + c added to an even number, minus the sum of the values of all the cells with r + c added to an odd number. Another way to look at it is that the sign of the first cell of a row is always the opposite of the first cell of the previous row. All subsequent cells in the same row will then be added to the checksum with alternating signs.

Only the lower 8 bits of the checksum are transmitted.

For example, the checksums for the sample puzzles shown in the Background page can be calculated as:

Puzzle	checksum
	- 1 + 4 - 5 + 2 + 9 - 3 - 9 - 4 + 5 - 1 + 5 + 8 - 6 + 7 + 3 - 7 + 6 - 2 - 5 + 1 - 3 + 4 + 4 - 3 + 6 + 2 - 8 + 2 - 7 - 4 - 5 + 1 + 5 - 2 + 8 - 4 = 3
	29

Hardware

To ensure a fair competition, the FPGA platform allowed for the competition is limited to a set of systems with similar capabilities. You may choose from any one of the approved FPGA boards listed below. Please contact one of us if you feel that a board with similar capabilities should be included.

The following is the list of currently approved systems:

Evaluation

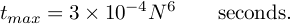A set of undisclosed puzzles will be used to evaluate your design. The test puzzles will have orders, N, ranging from 3 to 15. The maximum time allowed for solving a puzzle of order N is defined as $t_{max} = 3\times 10^{-4} N^6 \quad\quad \text{seconds.}$ This will limit the total run time for N=3 to be around 0.2 seconds, and for N=15 to be around 1 hour. If your solver does not correctly solve each of the evaluation puzzles for a given order within the allowed time, the contribution to the evaluation function for that order will be zero (0). That is, t_N is set to ∞. Furthermore, if your solver is not able to solve puzzles of a particular order, and thus not returning a correct solution within the maximum allowed time, t_N is set to ∞ as well.

Note that in order to facilitate our evaluation process, you need to submit together with your design the result of solving benchmark puzzles posted in this website using your solver. See Design Submission for details.

The time to solve a puzzle is defined as the time commencing with the transmission of the checksum byte at the end of the data input transmission and finishing with the receipt of the checksum byte at the start of the data output transmission. Therefore, the delay of the serial connection will not affect the timing significantly.

Sample puzzles and controlling software that will run on the host PC, will be posted in the Benchmarks page as soon as they are ready.